class Leap.Vector
The Vector object represents a three-component mathematical vector or point such as a direction or position in three-dimensional space.
The Leap software employs a right-handed Cartesian coordinate system. Values given are in units of real-world millimeters. The origin is centered at the center of the Leap device. The x- and z-axes lie in the horizontal plane, with the x-axis running parallel to the long edge of the device. The y-axis is vertical, with positive values increasing upwards (in contrast to the downward orientation of most computer graphics coordinate systems). The z-axis has positive values increasing away from the computer screen.
Constructor Top
| Vector () |
Static Properties & Enumerations Top
| Leap.Vector | backward | ||
| Leap.Vector | down | ||
| Leap.Vector | forward | ||
| Leap.Vector | left | ||
| Leap.Vector | right | ||
| Leap.Vector | up | ||
| Leap.Vector | xAxis | ||
| Leap.Vector | yAxis | ||
| Leap.Vector | zAxis | ||
| Leap.Vector | zero |
Properties Top
| Float | [0] | ||
| Float | [1] | ||
| Float | [2] | ||
| Float | x | ||
| Float | y | ||
| Float | z |
Methods Top
| Float | AngleTo (Leap.Vector other) | |
| Boolean | compare (Leap.Vector other) | |
| Leap.Vector | Cross (Leap.Vector other) | |
| Float | distanceTo (Leap.Vector other) | |
| Leap.Vector | dividedBy (Float scalar) | |
| Float | dot (Leap.Vector other) | |
| Boolean | isValid () | |
| Float | magnitude () | |
| Float | magnitudeSquared () | |
| Leap.Vector | minus (Leap.Vector other) | |
| Leap.Vector | multiply (Float scalar) | |
| Leap.Vector | normalized () | |
| Float | pitch () | |
| Leap.Vector | plus (Leap.Vector other) | |
| Float | roll () | |
| Float[] | toArray () | |
| String | toString () | |
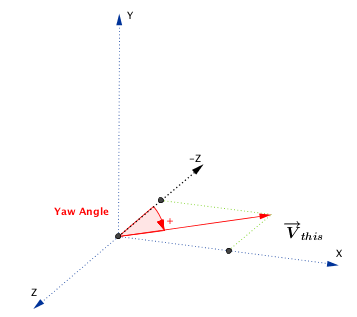
| Float | yaw () |
Constructor details
Top
vector.js at line 3
Vector
()
Constructs a Vector object.
Creates a new Vector from the specified Array or Vector.
The default constructor sets all components to zero.
Constructs a Vector object.
Creates a new Vector from the specified Array or Vector. The default constructor sets all components to zero.
Static Properties & Enumerations Detail Top
vector.js at line 376
The unit vector pointing backward along the positive z-axis: (0, 0, 1)
vector.js at line 385
The unit vector pointing down along the negative y-axis: (0, -1, 0)
vector.js at line 394
The unit vector pointing forward along the negative z-axis: (0, 0, -1)
vector.js at line 403
The unit vector pointing left along the negative x-axis: (-1, 0, 0)
vector.js at line 412
The unit vector pointing right along the positive x-axis: (1, 0, 0)
vector.js at line 421
The unit vector pointing up along the positive y-axis: (0, 1, 0)
vector.js at line 430
The x-axis unit vector: (1, 0, 0)
vector.js at line 439
The y-axis unit vector: (0, 1, 0)
vector.js at line 448
The z-axis unit vector: (0, 0, 1)
vector.js at line 457
The zero vector: (0, 0, 0)
Properties Detail Top
vector.js at line 44
public
Float
[0]
The horizontal component.
vector.js at line 57
public
Float
[1]
The vertical component.
vector.js at line 70
public
Float
[2]
The depth component.
vector.js at line 43
public
Float
x
The horizontal component.
vector.js at line 56
public
Float
y
The vertical component.
vector.js at line 69
public
Float
z
The depth component.
Methods Detail Top
vector.js at line 85
The angle between this vector and the specified vector in radians.
The angle is measured in the plane formed by the two vectors. The angle returned is always the smaller of the two conjugate angles. Thus A.angleTo(B) == B.angleTo(A) and is always a positive value less than or equal to pi radians (180 degrees).
If either vector has zero length, then this function returns zero.

vector.js at line 345
Compare Vector equality component-wise.
vector.js at line 109
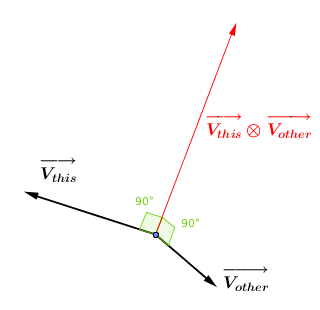
The cross product of this vector and the specified vector.
The cross product is a vector orthogonal to both original vectors. It has a magnitude equal to the area of a parallelogram having the two vectors as sides. The direction of the returned vector is determined by the right-hand rule. Thus A.cross(B) == -B.cross(A).
vector.js at line 132
The distance between the point represented by this Vector object and a point represented by the specified Vector object.
vector.js at line 198
Divide vector by a scalar.
vector.js at line 145
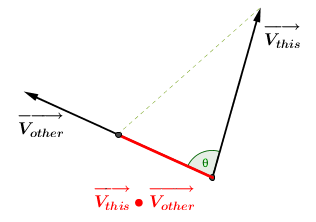
The dot product of this vector with another vector.
The dot product is the magnitude of the projection of this vector onto the specified vector.
vector.js at line 357
public
Boolean
isValid
()
Returns true if all of the vector's components are finite.
If any component is NaN or infinite, then this returns false.
vector.js at line 210
public
Float
magnitude
()
The magnitude, or length, of this vector.
The magnitude is the L2 norm, or Euclidean distance between the origin and the point represented by the (x, y, z) components of this Vector object.
vector.js at line 225
public
Float
magnitudeSquared
()
The square of the magnitude, or length, of this vector.
vector.js at line 174
Subtract vectors component-wise.
vector.js at line 186
Multiply vector by a scalar.
vector.js at line 236
A normalized copy of this vector.
A normalized vector has the same direction as the original vector, but with a length of one.
vector.js at line 253
public
Float
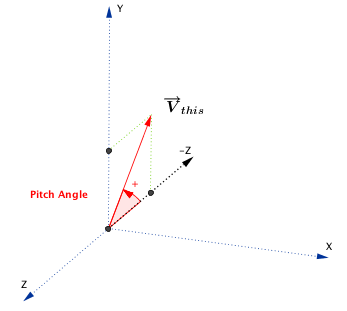
pitch
()
The pitch angle in radians.
Pitch is the angle between the negative z-axis and the projection of the vector onto the y-z plane. In other words, pitch represents rotation around the x-axis. If the vector points upward, the returned angle is between 0 and pi radians (180 degrees); if it points downward, the angle is between 0 and -pi radians.
vector.js at line 162
Add vectors component-wise.
vector.js at line 273
public
Float
roll
()
The roll angle in radians.
Roll is the angle between the y-axis and the projection of the vector onto the x-y plane. In other words, roll represents rotation around the z-axis. If the vector points to the left of the y-axis, then the returned angle is between 0 and pi radians (180 degrees); if it points to the right, the angle is between 0 and -pi radians.

Use this function to get roll angle of the plane to which this vector is a normal. For example, if this vector represents the normal to the palm, then this function returns the tilt or roll of the palm plane compared to the horizontal (x-z) plane.
vector.js at line 320
public
Float[]
toArray
()
Returns the vector as a float array.
vector.js at line 331
public
String
toString
()
Returns a string containing this vector in a human readable format: (x, y, z).
vector.js at line 299
public
Float
yaw
()
The yaw angle in radians.
Yaw is the angle between the negative z-axis and the projection of the vector onto the x-z plane. In other words, yaw represents rotation around the y-axis. If the vector points to the right of the negative z-axis, then the returned angle is between 0 and pi radians (180 degrees); if it points to the left, the angle is between 0 and -pi radians.